Mathematics: Số e

Hằng số toán học e là cơ số của logarit tự nhiên. Thỉnh thoảng nó được gọi là số Euler, đặt theo tên nhà toán học Thụy Sĩ Leonhard Euler, hoặc hằng số Napier để ghi công nhà toán học Scotland John Napier người đã phát minh ra logarit. (e không được nhầm lẫn với γ - hằng số Euler-Mascheroni, đôi khi được gọi đơn giản là hằng số Euler). Số e là một trong những số quan trọng nhất trong toán học ^[1]. Nó có một số định nghĩa tương đương, một số trong chúng sẽ được đưa ra dưới đây.
Số này có tham gia vào đẳng thức Euler.
Do e là số siêu việt, và do đó là số vô tỉ, giá trị của nó không thể được đưa ra một cách chính xác dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn hoặc phân số liên tục hữu hạn hay tuần hoàn. Nó là một số thực và do đó có thể được biểu diễn bởi một phân số liên tục vô hạn không tuần hoàn. Giá trị số của e tới 20 chữ số thập phân là:

2,71828 18284 59045 23536...

[sửa] Lịch sử

Chỉ dẫn tham khảo đầu tiên tới hằng số này được xuất bản vào 1618 trong bảng phụ lục của một công trình về logarit của John Napier. Thế nhưng, công trình này không chứa hằng số e, mà đơn giản chỉ là một danh sách các logarit tự nhiên được tính toán từ hằng số e. Có thể là bảng này được soạn bởi William Oughtred. Chỉ dẫn đầu tiên cho biết về hằng số e được phát hiện bởi Jacob Bernoulli, trong khi tìm giá trị của biểu thức:

$\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$

Việc sử dụng đầu tiên ta từng biết của hằng số, biểu diễn bởi chữ cái b, là trong liên lạc thư từ giữa Gottfried Leibniz và Christiaan Huygens giữa 1690 và 1691. Leonhard Euler bắt đầu sử dụng chữ cái e cho hằng số vào 1727, và việc sử dụng e lần đầu tiên trong một ấn bản là cuốn Mechanica của Euler (1736). Trong những năm sau đó một số nhà nghiên cứu sử dụng chữ cái c, e trở nên phổ biến và cuối cùng trở thành tiêu chuẩn.
Lí do chính xác cho việc sử dụng chữ cái e vẫn chưa được biết, nhưng có thể đó là chữ cái đầu tiên của từ exponential (tiếng Anh: nghĩa thông thường là tăng nhanh chóng, nghĩa trong toán học là hàm mũ). Một khả năng khác đó là Euler sử dụng nó bởi vì nó là nguyên âm đầu tiên sau a, chữ cái mà ông đã sử dụng cho một số khác, nhưng tại sao ông lại sử dụng nguyên âm thì vẫn chưa rõ. Dường như không phải Euler sử dụng chữ cái đó bởi vì nó là chữ cái đầu trong tên của ông, do ông là một người rất khiêm tốn, luôn cố gắng tuyên dương đúng đắn tới các công trình của người khác.^[2]

[sửa] Ứng dụng

[sửa] Bài toán lãi suất kép

Jacob Bernoulli đã khám phá ra hằng số này khi nghiên cứu vấn đề về lãi suất kép
Một ví dụ đơn giản là một tài khoản bắt đầu với $1.00 và trả 100% lợi nhuận mỗi năm. Nếu lãi suất được trả một lần, thì đến cuối năm giá trị là $2.00; nhưng nều lãi suất được tính và cộng hai lần trong năm, thì $1 được nhân với 1.5 hai lần, ta được $1.00×1.5² = $2.25. Lãi kép hàng quí ta được $1.00×1.25⁴ = $2.4414…, và lãi kép hàng tháng ta được $1.00×(1.0833…)¹² = $2.613035….
Bernoulli để ý thấy dãy này tiến tới một giới hạn với kì lãi kép càng ngày nhỏ dần. Lãi kép hàng tuần ta được $2.692597… trong khi lãi kép hàng ngày ta được $2.714567…, chỉ thêm được hai cent. Gọi n là số kì lãi kép, với lãi suất 1/n trong mỗi kì, giới hạn của n rất lớn là một số mà bây giờ ta gọi là số e; với lãi kép liên tục, giá trị tài khoản sẽ tiến tới $2.7182818…. Tổng quát hơn, một tài khoản mà bắt đầu bằng $1, và nhận được (1+R) đô-la lãi đơn, sẽ nhận được e^R đô-la với lãi kép liên tục.

[sửa] Phép thử Bernoulli

Số e cũng có ứng dụng trong lý thuyết xác suất, trong đó nó phát triển theo cách mà không hiển nhiên liên quan đến độ tăng hàm mũ. Giả sử rằng một con bạc chơi slot machine, một triệu lần, kỳ vọng được thắng một lần. Khi đó xác suất mà con bạc không thắng được gì là (xấp xỉ) 1/e.
Đây là một ví dụ về phép thử Bernoulli. Mỗi lần con bạc chơi một lượt, có thêm một trong một triệu cơ hội thắng. Việc chơi một triệu lần được mô hình hóa qua phân phối nhị thức, có liên hệ mật thiết với định lý nhị thức. Xác suất thằng k lần và thua các lần còn lại là

$\binom{10^6}{k} \left(10^{-6}\right)^k(1-10^{-6})^{10^6-k}.$

Đặc biệt, xác suất không thắng lần nào (k=0) là

$\left(1-\frac{1}{10^6}\right)^{10^6}.$

Số này rất gần với giới hạn sau ho 1/e

$\frac{1}{e} = \lim_{n\to\infty} \left(1-\frac{1}{n}\right)^n.$

[sửa] Derangement

[sửa] Số e trong giải tích

Lý do chính để đưa ra số e, đặc biệt trong giải tích, là để lấy vi phân và tích phân của hàm mũ và logarit.^[3] Một hàm mũ tổng quát y=a^x có đạo hàm dưới dạng giới hạn:

$\frac{d}{dx}a^x=\lim_{h\to 0}\frac{a^{x+h}-a^x}{h}=\lim_{h\to 0}\frac{a^{x}a^{h}-a^x}{h}=a^x\left(\lim_{h\to 0}\frac{a^h-1}{h}\right).$

Giới hạn ở bên phải độc lập với biến x: nó chỉ phụ thuộc vào cơ số a. Khi cơ số là e, giới hạn này tiến tới một, và do đó e được định nghĩa bởi phương trình:

$\frac{d}{dx}e^x = e^x.$

Do đó, hàm mũ với cơ số e trong một số trường hợp phù hợp để làm giải tích. Chọn e, không như một số số khác, là cơ số của hàm mũ làm cho tính toán chủ yếu về đạo hàm đơn giản hơn rất nhiều.
Một lý do khác đến từ việc xét cơ số logarit a.^[4] Xét định nghĩa của đạo hàm của log_ax bởi giới hạn:

$\frac{d}{dx}\log_a x = \lim_{h\to 0}\frac{\log_a(x+h)-\log_a(x)}{h}=\frac{1}{x}\left(\lim_{u\to 0}\frac{1}{u}\log_a(1+u)\right).$

Một lần nữa, có một giới hạn chưa xác định mà chỉ phụ thuộc vào cơ số a, và nếu cơ số đó là e, giới hạn là một. Vậy

$\frac{d}{dx}\log_e x=\frac{1}{x}.$

Logarit trong trường hợp đặc biệt này được gọi là logarit tự nhiên (thường được kí hiệu là "ln"), và nó cũng dễ dàng lấy vi phân vì không có giới hạn chưa xác định nào phải thực hiện trong khi tính toán.
Do đó có hai cách để chọn một số đặc biệt a=e. Một cách là đặt sao cho đạo hàm của hàm số a^x là a^x. Một cách khác là đặt sao cho đạo hàm của logarit cơ số a là 1/x. Mỗi trường hợp đều đi đến một lựa chọn thuận tiện để làm giải tích. Thực tế là, hai cơ số có vẻ rất khác nhau này lại chỉ là một, số e.

[sửa] Các đặc điểm khác

Một số đặc điểm khác của số e: một là về giới hạn dãy, một cái khác là về chuỗi vô hạn, và vẫn còn một số khác về tích phân. Trên đây ta đã giới thiệu hai tính chât:
1. Số e là số thực dương duy nhất mà

$\frac{d}{dt}e^t = e^t.$ : Đạo hàm của hàm số mũ cơ số e chính là hàm số đó

2. Số e là số thực dương duy nhất mà

$\frac{d}{dt} \log_e t = \frac{1}{t}.$

Các tính chất khác sau đây cũng được chứng minh là tương đương:
3. Số e là giới hạn

$e = \lim_{n\to\infty} \left( 1 + \frac{1}{n} \right)^n$

4. Số e là tổng của chuỗi vô hạn

$e = \sum_{n = 0}^\infty \frac{1}{n!} = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdots$

trong đó n! là giai thừa của n.
5. Số e là số thực dương duy nhất mà

$\int_{1}^{e} \frac{1}{t} \, dt = {1}$

(nghĩa là, số e là số mà diện tích dưới hyperbol

f (t) = 1 / t

từ 1 tới e là bằng một)

[sửa] Tính chất

[sửa] Hàm tựa-mũ

[sửa] Lý thuyết số

Chứng minh e là số vô tỉ.
Giả sử e là số hữu tỉ, suy ra

$e = \frac{p}{q}$

Dựa vào công thức:

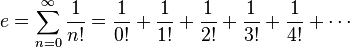$e = \sum_{n = 0}^\infty \frac{1}{n!} = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdots$ .

$e.q! = (\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \cdots).q! = (\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \cdots + \frac{1}{q!}) . q! + \frac{1}{q+1} + \frac{1}{(q+1)(q+2)} + \frac{1}{(q+1)(q+2)(q+3)} + \cdots$

e.q! là số nguyên dương, suy ra: $\frac{1}{q+1} + \frac{1}{(q+1)(q+2)} + \frac{1}{(q+1)(q+2)(q+3)} + \cdots$ là số nguyên dương.
Mặt khác: $\frac{1}{q+1} + \frac{1}{(q+1)(q+2)} + \frac{1}{(q+1)(q+2)(q+3)} + \cdots < \frac{1}{q+1} - \frac{1}{q+2} + \frac{1}{q+2}-\frac{1}{q+3} + ... < \frac{1}{q+1} < 1$ .
Suy ra điều mâu thuẫn.
Vậy e là số vô tỉ.

[sửa] Số phức

[sửa] Biểu diễn của số e

[sửa] Biểu diễn số e dưới dạng liên phân số

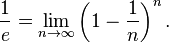
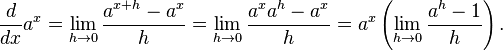
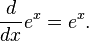
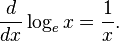
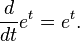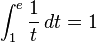
$e = [[2; 1, \textbf{2}, 1, 1, \textbf{4}, 1, 1, \textbf{6}, 1, 1, \textbf{8}, 1, \ldots,1, \textbf{2n}, 1,\ldots]], \,$

$e=2+ \cfrac{1}{ 1+\cfrac{1}{ {\mathbf 2}+\cfrac{1}{ 1+\cfrac{1}{ 1+\cfrac{1}{ {\mathbf 4}+\cfrac{1}{ \ddots } } } } } }$

Như vây mặc dù e là số vô tỉ nhưng trong biểu diễn liên phân số lại phân phối theo qui luật tuyến tính: 2;1-2-1;1-4-1;1-6-1;1-8-1;...
Theo vi.wikipedia.org

Mathematics

Trang

Sunday, July 4, 2010

Số e

Mục lục