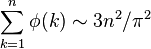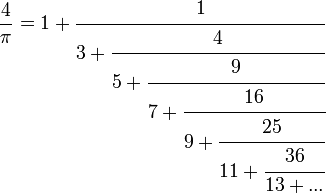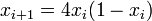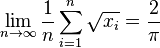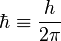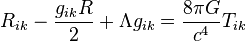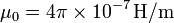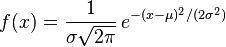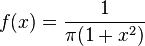Mathematics: Số Pi

Pi là một hằng số trong toán học có giá trị bằng chu vi đường tròn đường kính của đường tròn đó. Nó hay được viết ký hiệu bằng chữ Hy Lạp π. Tên pi do chữ peripheria (perijeria) có nghĩa là chu vi của đường tròn.

Trong thực tế, để tính toán, người ta thường dùng giá trị gần đúng là 3,14 hoặc 3,1416. Trong những lĩnh vực cần độ chính xác cao hơn, như trong hàng không vũ trụ, pi được dùng không quá 10 chữ số thập phân.
Trong nhiều ngôn ngữ như tiếng Anh, Pháp, Nga, Đức, người ta đã đặt ra những đoạn văn hoặc thơ ngắn để giúp nhớ số Pi. Một bài thơ tiếng Nga dịch ra tiếng Việt có nghĩa là "Một điều tôi biết và rất nhớ, là Pi có nhiều chữ số thừa, vô dụng đối với tôi." (theo Hình học giải trí, NXB Cầu Vồng).
Giá trị số của Pi viết đến 100 chữ số thập phân là:

3, 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679...

Trong toán học, Pi là số vô tỉ. Phân loại chi tiết hơn, Pi là một số siêu việt.

Một định nghĩa trực quan về giá trị số của Pi, bằng độ dài của đường tròn có đường kính là 1.

Lịch sử

Số π đã được người cổ Ai Cập và Babylon biết đến mặc dù lúc đó giá trị của nó không được chính xác như ngày nay. Chẳng hạn người Babylon cho rằng nó vào khoảng 3 1/8 (3,125) và người Ai Cập thì rằng nó vào khoảng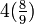 $4(\tfrac{8}{9})$ ≈3,160484.
Ác si mét (287-212 TCN) là người đầu tiên tính chính xác số π, ông cho rằng chu vi đường tròn bị giới hạn bởi đa giác nội tiếp và ngoại tiếp đường tròn. Sử dụng đa giác 96 cạnh ông chứng minh được rằng 223/71 < π < 22/7, giá trị của π là 3.1419.
Ở Trung Quốc, đến thời Đông Hán, Trương Hạnh (Zhang Heng, 78 - 139) cho rằng π là căn bậc 2 của 10. Thời Ngụy Tấn (khoảng năm 263), nhà toán học Lưu Huy (Liu Hui) đã chỉ ra rằng "chu tam kinh nhất" chỉ là tỉ lệ chu vi của hình lục giác đều nội tiếp và đường kính của đường tròn. Về sau, khi dùng phương pháp cát tuyến, ông đã tính được chu vi của hình 3072 cạnh nội tiếp, ống tính ra được giá trị của π là 3,1416.
Đến thời Nam Bắc triều, khoảng năm 480, nhà khoa học Tổ Xung Chi (Zu Chongzhi, 429 - 500) tìm ra số π = 355/113 <=> 3,1415926 < π < 3,1415927. Ông tìm ra số π dựa trên thuật toán của Lưu Huy tính với đa giác nội tiếp 12288 cạnh. Số π do Tổ Xung Chi tìm ra chính xác nhất trong vòng 900 năm sau đó.
Kí hiệu π được William Jones dùng đầu tiên vào năm 1706, ông đã viết như sau:

There are various other ways of finding the Lengths or Areas of particular Curve Lines, or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to the Circumference as 1 to 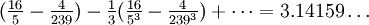$(\tfrac{16}{5} - \tfrac{4}{239}) - \tfrac{1}{3} (\tfrac{16}{5^3} - \tfrac{4}{239^3}) + \cdots = 3.14159\ldots$ (trích A History of Mathematical Notation của Florian Cajori, ISBN 0-486-67766-4)

Tạm dịch:

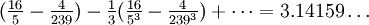"Có nhiều cách để tìm Chu vi hay Diện tích của các Đường cong đặc thù, hay các Hình phẳng mà rất tiện lợi trong thực hành; chẳng hạn như, trong Hình tròn, có đường kính là 1 thì giá trị chu vi là $(\tfrac{16}{5} - \tfrac{4}{239}) - \tfrac{1}{3} (\tfrac{16}{5^3} - \tfrac{4}{239^3}) + \cdots = 3.14159\ldots$ "

Trong thời gian Euler còn sống chính nhà toán học này đã đưa giả định rằng "π không là nghiệm của một phương trình đại số". Tức là, π, cùng với số e, là số siêu việt.
Mãi đến nửa cuối thế kỷ 19, năm 1882, nhà toán học Ferdinand von Lindemann mới chứng minh được giả định trên là đúng dựa vào một lập luận trong hình học phẳng "bình phương của một hình tròn là không giải được". (Xem thêm chi tiết trong chương 3 của cuốn Mathematics from the Birth of Numbers của Jan Gullberg, ISBN 0-393-04002-X.)
Ngày nay, dùng máy tính người ta tìm được đến hơn 50.000 số lẻ của Pi. [1]
Ngày 22 tháng 9 năm 1997, Fabrice Bellard đã tính được số lẻ thứ một ngàn tỉ.
Tháng 2 năm 1999, Colin Percival đã tính được con số lẻ thứ bốn mươi ngàn tỉ.
Ngày 11 tháng 9 năm 2000: con số lẻ thứ một triệu tỉ là số không (zero): (một triệu tỉ =1.000.000.000.000.000)

Tính Pi

Archimedes tính Pi bằng đa giác đều

Bằng cách nội tiếp và ngoại tiếp đường tròn bởi một đa giác 96 cạnh ông đã rút ra được:
3 + 10/71 < π < 3 + 1/7

Tính pi thời xưa

Trải qua nhiều năm lịch sử, người ta đã mất rất nhiều công thức để tính Pi, dù chỉ là giá trị gần đúng. Sau đây là một ví dụ:

Người La Mã lấy pi ≈ 3,12
Người Ai Cập Cổ đại cho rằng pi ≈ 3,16
Người Babylon lấy pi ≈ 3,125
Ác si mét tính được pi ≈ 3,1428
Trương Hành ( Trung Quốc ) lấy pi ≈ √10 ≈ 3,162
Tổ Xung Chi lấy pi ≈ 3,1415926 (Điều đặc biệt là số này khá gần với giá trị pi chuẩn)
Ở Việt Nam, các cụ lấy pi ≈ 3,2
Lam be (Người Đức) chứng minh được pi là số vô tỉ
Ru đôn phơ (Người Đức) tính được pi với 35 chữ số thập phân. Giá trị này đã được khắc lên mộ ông theo lời đề nghị.
Lin đơ man (Người Đức - Lại là người Đức!) chứng minh thành công pi là số siêu việt.
Đến 1989, bằng máy tính điện tử, pi được tính với 4 tỉ chữ số thập phân!!!

Công thức có dùng số π

Hình học

π

có mặt trong hình học liên quan tới hình tròn và hình cầu:

Dạng hình	Công thức
Chu vi hình tròn bán kính r và đường kính d	$C = \pi d = 2 \pi r \,\!$
Diện tích hình tròn bán kính r	$A = \pi r^2 \,\!$
Diện tích hình ellipse với các bán trục a và b	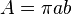$A = \pi a b \,\!$
Thể tích hình cầu bán kính r và đường kính d	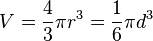$V = \frac{4}{3} \pi r^3 = \frac{1}{6} \pi d^3 \,\!$
Diện tích bề mặt hình cầu bán kính r	$A = 4 \pi r^2 \,\!$
Thể tích hình lăng trụ chiều cao h bán kính r	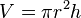$V = \pi r^2 h \,\!$
Diện tích bề mặt hình lang trụ cao h bán kính r	$A = 2 (\pi r^2) + (2 \pi r) h = 2 \pi r (r + h) \,\!$
Thể tích hình nón cao h bán kính r	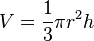$V = \frac{1}{3} \pi r^2 h \,\!$
Thể tích hình nón cụt cao H bán kính lớn R bán kính nhỏ r	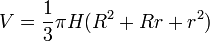$V = \frac{1}{3} \pi H (R^2 + Rr + r^2) \,\!$ HMT
Diện tích bề mặt hình nón cao h và bán kính r	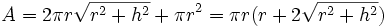$A = 2 \pi r \sqrt{r^2 + h^2} + \pi r^2 = \pi r (r + 2 \sqrt{r^2 + h^2}) \,\!$

Ngoài ra, góc đo 180° thì bằng với π rad.

Giải tích

Nhiều công thức giải tích chứa π bao gồm các biểu thức chuỗi vô hạn (và tích vô hạn), tích phân, và cái gọi là các hàm đặc biệt.

François Viète, 1593 (chứng minh):

$\frac2\pi= \frac{\sqrt2}2 \frac{\sqrt{2+\sqrt2}}2 \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\ldots$

Công thức Leibniz (chứng minh):

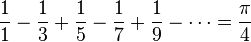
$\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$
Một cách kĩ thuật thì chuỗi trên được biểu thị dưới dạng:
$\sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1} = \frac{\pi}{4}$

Tích Wallis:

$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$
$\prod_{n=1}^{\infty} \frac{(2n)^2}{(2n)^2-1} = \prod_{n=1}^{\infty} \frac{2n}{2n-1} \cdot \frac{2n}{2n+1} = \frac{\pi}{2}$

Thuật toán Bailey-Borwein-Plouffe (năm 1995)

$\pi=\sum_{k=0}^\infty\frac{1}{16^k}\left [ \frac {4}{8k+1} - \frac {2}{8k+4} - \frac {1}{8k+5} - \frac {1}{8k+6}\right ]$

Công thức tích phân từ giải tích (xem thêm Hàm lỗi và phép Phân phối chuẩn):

$\int_{-\infty}^{\infty} e^{-x^2}\,dx = \sqrt{\pi}$

Vấn đề Cơ bản 1, đầu tiên được giải bởi Euler (xem thêm Hàm Riemann zeta):

$\zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$
$\zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}$
and generally, $ζ(2 n)$ is a rational multiple of $π 2 n$ for positive integer n

Hàm Gamma ở giá trị 1/2:

$\Gamma\left({1 \over 2}\right)=\sqrt{\pi}$

Phép gần đúng Stirling:

$n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n$

Phương trình nhận diện Euler (Richard Feynman đặt tên, là "công thức quan trọng nhất của toán học"):

$e^{i \pi} + 1 = 0\;$

Tính chất của hàm Euler (xem thêm dãy Farey):

$\sum_{k=1}^{n} \phi (k) \sim 3 n^2 / \pi^2$

Diện tích 1/4 của hình tròn đơn vị:

$\int_0^1 \sqrt{1-x^2}\,dx = {\pi \over 4}$

Một áp dụng của định lý thặng dư

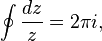
$\oint\frac{dz}{z}=2\pi i,$
Đường cong tích phân xung quanh gốc tọa độ, và có hướng ngược chiều kim đồng hồ.

Liên phân số

π có mặt trong nhiều biểu thức liên phân số chẳng hạn như:

$\frac{4}{\pi} = 1 + \cfrac{1}{3 + \cfrac{4}{5 + \cfrac{9}{7 + \cfrac{16}{9 + \cfrac{25}{11 + \cfrac{36}{13 + ...}}}}}}$

Lý thuyết số

Các kết quả sau đây trong lý thuyết số:

Xác suất để hai số nguyên được chọn ngẫu nhiên là nguyên tố cùng nhau là $\begin{matrix} \cfrac{6}{\pi^2} \end{matrix}$ .

Xác suất để một số nguyên được chọn ngẫu nhiên nó không chia hết cho một số chính phương là $\begin{matrix} \cfrac{6}{\pi^2} \end{matrix}$ .

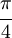Giá trị trung bình của các cách viết một số nguyên dương như là tổng của hai số chính phương (có tính đến thứ tự) là $\begin{matrix} \cfrac{\pi}{4} \end{matrix}$ .

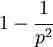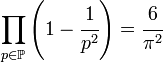
Tích ( $\begin{matrix} 1-\cfrac{1}{p^2} \end{matrix}$ ), trong đó p là số nguyên tố, là $\begin{matrix} \cfrac{6}{\pi^2} \end{matrix}$ . $\prod_{p\in\mathbb{P}} \left(1- \cfrac{1}{p^2} \right) = \cfrac {6} {\pi^2}$

Ở đây sác xuất được tính trên tập N các số tự nhiên.
Một sự thật quan trọng là

$e^{\pi \sqrt{163}} = 262537412640768743,99999999999925007...$

hay tương đương với nó,

$e^{\pi \sqrt{163}} = 640320^3+743,99999999999925007...$

có thể được giải thích bởi lí thuyết phép nhân số phức.

[sửa] Các hệ thống động học và lý thuyết ergo

Xét công thức truy hồi

$x_{i+1} = 4 x_i (1 - x_i) \,$

Khi đó cho hầu như mỗi giá trị ban đầu x₀ trong hệ đoạn thẳng đơn vị [0,1],

$\lim_{n \to \infty} \frac{1}{n} \sum_{i = 1}^{n} \sqrt{x_i} = \frac{2}{\pi}$

với quan hệ truy hồi này thì ánh xạ logistic với tham số r = 4, đã biết từ định lý về các hệ thống động học. Xem thêm lý thuyết ergo.

Vật lý

Số π xuất hiện trong các phương trình mô tả các nguyên lý nền tảng của vũ trụ, một phần không nhỏ do mối quan hệ tự nhiên của nó với hình tròn và tương ứng là các hệ tọa độ cầu.

Hằng số vũ trụ:

$\Lambda = {{8\pi G} \over {3c^2}} \rho$

Hằng số Planck-Dirac:

$\hbar\equiv\frac{h}{2\pi}$

Nguyên lý bất định Heisenberg:

$\Delta x \Delta p \ge \frac{h}{4\pi}$

Phương trình trường Einstein trong Thuyết tương đối tổng quát:

$R_{ik} - {g_{ik} R \over 2} + \Lambda g_{ik} = {8 \pi G \over c^4} T_{ik}$

Định luật Coulomb về lực điện từ:

$F = \frac{\left|q_1q_2\right|}{4 \pi \epsilon_0 r^2}$

Tích từ thẩm trong không gian tự do:

$\mu_0 = 4 \pi \times 10^{-7}\,\mathrm{H/m}\,$

Xác suất và thống kê

Trong xác suất và thống kê, có nhiều công thức phân bố chứa số π trong đó có:

Hàm mật độ xác suất (pdf, viết tắt từ chữ probability density function) trên phân phối chuẩn với giá trị trung bình μ và độ lệch chuẩn σ:

$f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-(x-\mu)^2/(2\sigma^2)}$

pdf trong (chuẩn) phân phối Cauchy:

$f(x) = \frac{1}{\pi (1 + x^2)}$

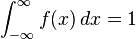Lưu ý: vì $\int_{-\infty}^{\infty} f(x)\,dx = 1$ , cho mọi pdf f(x), công thức trên có thể được dùng để suy ra các công thức tích phân khác cho số π.
Theo http://vi.wikipedia.org

Mathematics

Trang

Sunday, July 4, 2010

Số Pi

Pi là một hằng số trong toán học có giá trị bằng chu vi đường tròn đường kính của đường tròn đó. Nó hay được viết ký hiệu bằng chữ Hy Lạp π. Tên pi do chữ peripheria (perijeria) có nghĩa là chu vi của đường tròn.

Lịch sử